How to make a square from a circle. |
|
The ancient Greeks tried to do all their drawings just using a straight edge and a pair of compasses, but one of the things they found impossible was drawing a square that has exactly the same area as a circle. The Murderous Maths Organisation likes a challenge, so we solved the unsolved problem.
1/
We need to start with a circle. If the diameter =1, then the circumference =
p.
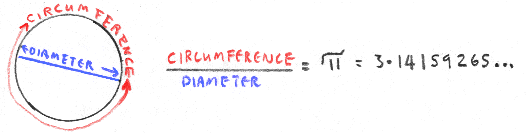
The formula for the area of any circle is pd2 / 4, so if d=1, the area of our circle = p/4. Our first job will be to make a rectangle with this same area. If we have a rectangle measuring p along the bottom and 1/4 up the side then that'll do it! |
2/
In the book we show how to convert the circumference of the circle into a straight line of length p. That's the tricky part that the Greeks couldn't do but we used a secret weapon - A TIN OF BEANS!
| ||
| |||
|
3/
To make our rectangle, we start by drawing a line of length p and then construct a right angle at one end.
|
4/
Now we need to get a line of length 1/4. We get this by bisecting the diameter of the circle twice. (Remember the diameter = 1) Once we've done this we can use it to set our compasses to a length of 1/4.
| ||
|
5/
Here's how to make the rectangle with area p/4. We continue with our line that has the right angle constructed on the end.
This rectangle has the same area as the circle. |
6/
So far so good. Now we need to convert this rectangle into a square of the same area p/4. This is a pretty good trick on its own!
| ||
And that's how we solved one of the great UNSOLVED problems of antiquity using our SECRET WEAPON. It's such a brilliant weapon that we're surprised that the ancient Greeks didn't think of it first!
If you enjoyed this page, find out how we TRISECT AN ANGLE!
