How to turn a rectangle into a square of the same area.

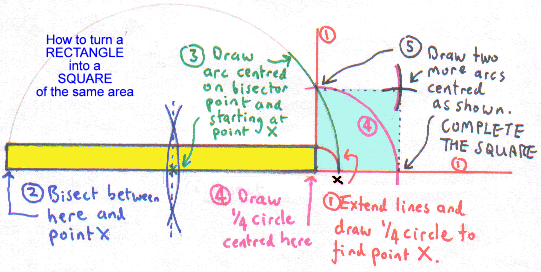
In The Murderous Maths of Everything we meet the ancient Greek mathematicians. They liked to solve problems only using a pair of compasses and a straight edge. Some of the tricks they invented were ingenious, and this is one of our favourites!

Many thanks to MICHAEL JONES for supplying a neat little proof as to why this works!

Call the long side of the rectangle a and the short side b. The sides of the square are s. For the areas of the rectangle and square to be the same then ab must equal s2.

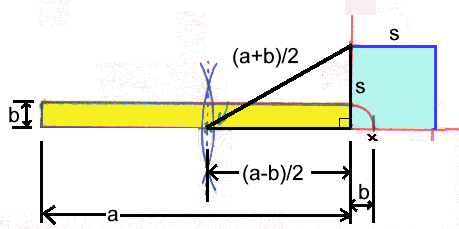
If you make a little right angled triangle as shown, the hypotenuse (the longest side) = (a+b)/2 and one of the short sides is (a-b)/2. The other short side is s.

Pythagoras Theorem says that s2 = [(a+b)/2]2 - [(a-b)/2]2

If we bang this through...

s2 = (a2 +2ab + b2)/4 - (a2 -2ab + b2)/4

s2 = (a2 +2ab + b2 - a2 + 2ab - b2)/4

s2 = 4ab/4

s2 = ab

...and that's what we wanted!


The Murderous Maths of Everything

Vicious Circles and other Savage Shapes

Murderous Maths Home Page