How do we work it out?
|
|
|
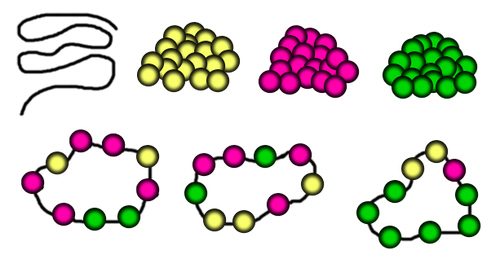
First lay out your necklace as a long straight string (we'll figure out later what happens when you join the ends to make it into a circle). Suppose your three colours of beads are yellow, green and red. Any of the beads can be any of the three colours, so the total number of possible string patterns is 39 = 19,683...
|
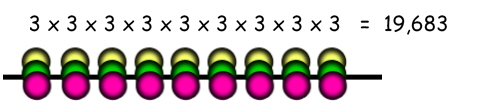
|
|
... BUT ...
| |
|
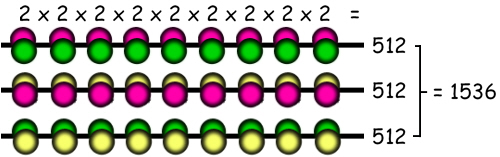
... you only want the strings that use all three colours. Some of those 19,683 strings only use two colours. So how many two colour strings are there? There are 29 which only use red and green, 29 which only use yellow and red, and 29 which only use green and yellow. So we need to subtract 3 x 29 = 1,536 from the total. This gives us 19,683 - 1,536 = 18,147 ...
|
|
|
... BUT ...
| |
|
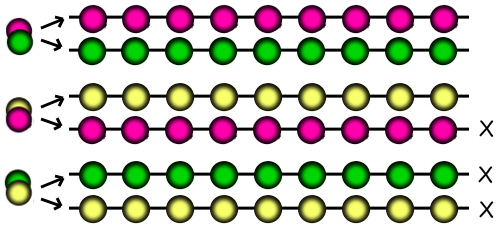
... when we calculated the number of red and green strings, the total of 512 included a string with all reds and a string with all greens. Likewise, the calculation for yellow/red strings includes a string with all yellows and a string with all reds, and the green/yellow strings includes all greens and all yellows. Therefore we've subtracted the number of strings which are all the same colour twice.
 To compensate for this, we need to add three back. 18,147 + 3 = 18,150
To compensate for this, we need to add three back. 18,147 + 3 = 18,150
|
|
|
So the number of different strings of nine beads with three colours = 18,150.
| |
|
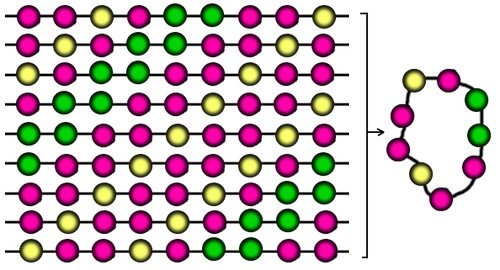
Next we need to work out how this number is reduced when you join the ends of the string together to make a necklace.
In most cases, there are nine different strings that will form the same necklace.
(You might prefer to think of this the other way round - If you take a necklace, you can break it at any one of the nine gaps and so form nine different strings.)
As we have 18,150 different strings, it's tempting to think that the number of different necklaces they can form is 18,150 ÷ 9...
|
|
|
... BUT ...
| |
|
... there's a slight problem here because 18,150 does not divide by 9. (In fact 18,150 ÷ 9 = 2016.6667 and having 0.6667 patterns of a necklace doesn't make sense!)
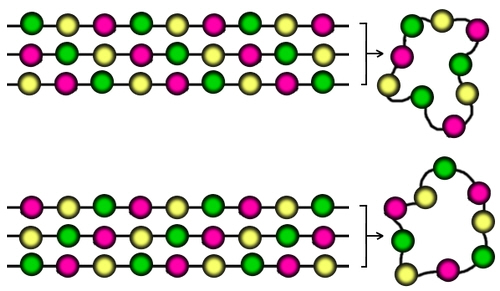
What's going on? The answer is that there are some necklaces which cannot be made from nine different strings. These necklaces are the ones that repeat in a three-bead pattern.
So how many necklaces can be formed from a three-bead repeating pattern? The answer is nice and simple - there are only TWO! (The beads go Green-Yellow-Red in sequence, or Red-Yellow-Green in sequence. Look at the diagram.) Creating these two necklaces uses six of our strings.
|
|
|
So...
- Our total number of different three-bead strings is 18,150.
- 6 of these strings create 2 different necklaces. (Remember that 2. We need it soon.)
- This leaves us with 18,150 - 6 = 18,144 strings.
- The total number of necklaces we can form with these strings is 18,144 ÷ 9 =
2016.
- Therefore...
The total number of necklaces we can make altogether is 2016 + 2 = 2018*
|
|

| |
With many thanks to Michael Jones
who worked all this out and
explained it so nicely!
|
|
|
|
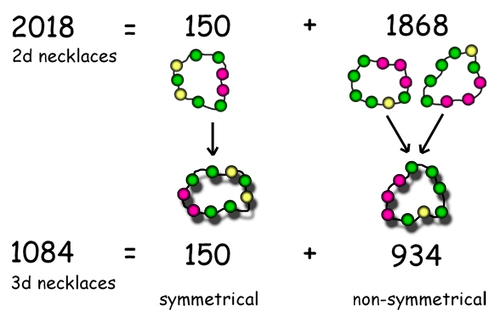
* This answer of 2018 only applies to necklaces drawn on paper or shown on a screen in 2d.
|
|
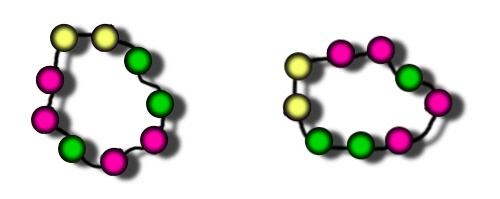
These two necklaces look different in 2 dimensions because starting with the two yellows and working clockwise, one goes yellow-yellow-green-green, and the other goes yellow-yellow-red-red. However if they were made up into real 3-dimensional necklaces, they would be identical. That's because you could flip one over to get the other. Another way of looking at it is that if you dropped them both into a box then picked them out, you couldn't tell which was which.
Our answer of 2018 treats these as two different necklaces, but in 3d it's the same one. It's tempting to think that the number of different 3d necklaces must be 2018 ÷ 2 = 1009, but surprise surprise it's not quite that easy!
|
|
|
|
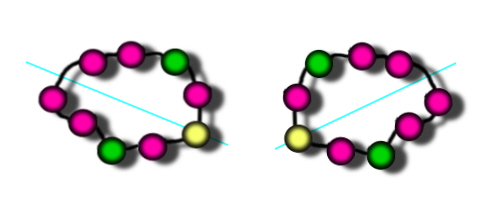
These pictures show the same necklace flipped over, but if you work round the colours in a clockwise direction, the sequence is the same (R-R-R-R-G-R-Y-R-G). That's because this necklace is symmetrical. If you draw a line through the yellow bead, you'll see the two sides both go yellow-red-green-red-red.
Therefore although non-symmetrical 3d necklaces each produce two different 2d necklaces, a symmetrical 3d necklace only produces one 2d necklace.
|
|
|
|
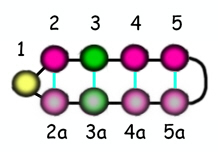 We now need to know how many of our 2018 necklaces are symmetrical. We now need to know how many of our 2018 necklaces are symmetrical.
To do this we just need to work out how many different ways the first five beads can be arranged. The pattern of the remaining four beads is then an exact copy.
|
|
|
We can work out the number of 5-bead 3-colour necklaces in exactly the same way as we worked out 18,150 above.
35 - 3 x 25 + 3 = 243 - 96 + 3 = 150
So out of our 2018 2d necklaces, 150 are symmetrical and each needs its own 3d necklace to create it. This means we have (2018-150 =) 1868 non-symmetrical 2d necklaces. The number of 3d necklaces needed to create them is 1868 ÷ 2 = 934.
If we add 150 + 934 we find the total number of 3-colour 9-bead real three-dimensional necklaces is 1084!
|
|


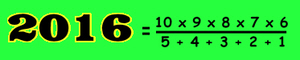










 The NINE BEAD NECKLACE!
The NINE BEAD NECKLACE!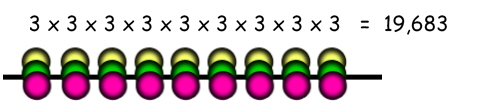

 To compensate for this, we need to add three back. 18,147 + 3 = 18,150
To compensate for this, we need to add three back. 18,147 + 3 = 18,150






 We now need to know how many of our 2018 necklaces are symmetrical.
We now need to know how many of our 2018 necklaces are symmetrical.

