
 The (Amazing) Alternate Segment Theorem!
The (Amazing) Alternate Segment Theorem!
 The (Amazing) Alternate Segment Theorem!
The (Amazing) Alternate Segment Theorem!
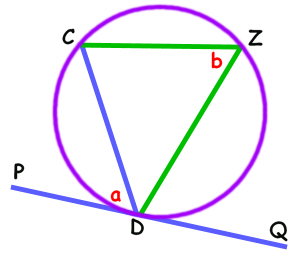
Here's the funny bit:
The angle between the chord and the tangent is ALWAYS equal to the angle "in the alternate segment".
In other words, in our diagram, angle a is always the same as angle b.
If you're not sure what segments or chords are look at our guide to Names of Bits of Circles

If you've read Savage Shapes, you'll know that you're not allowed just to say something without explaining why it always works, so here's the proof. (You might want your copy of Savage Shapes handy to check on some of the details we're about to use.)
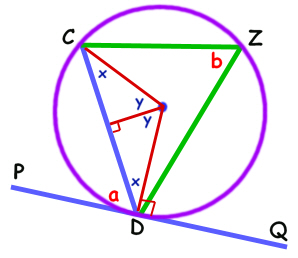 We've drawn a couple of radii (i.e. lines from the centre of the circle, we've made them
red for clarity)
to the ends of the chord.
This makes an isosceles triangle with two equal angles which we've marked "x".
(See page 104 of Savage Shapes.)
We've drawn a couple of radii (i.e. lines from the centre of the circle, we've made them
red for clarity)
to the ends of the chord.
This makes an isosceles triangle with two equal angles which we've marked "x".
(See page 104 of Savage Shapes.)
We split the isosceles triangle into two identical little right angled triangles. Each of them has an angle y at the centre of the circle.
The angle between the radius and the tangent is 90º (see page 114).
Now we just play with the angles a bit:
|
|
|
You can go on to show that this theorem works for the angles over 90º too!
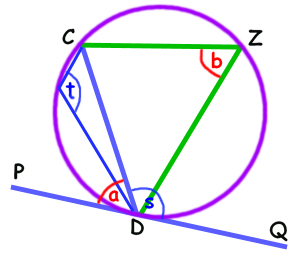
In this case, now we know that a = b we can show that s = t.
This is clever stuff - so if you've understood it WELL DONE!
