GCSE: Slips and Tips

We couldn't possibly try to show you everything you need to know for GCSE maths on this page, but hopefully it will give you a few ideas on...

HOW NOT TO THROW AWAY MARKS IN YOUR EXAM!

There's nothing more agonising than doing all your work for an exam and then doing something silly to ruin your answers at the very last minute. (Trust us - we know.) Therefore we've been in touch with Brian Speed who is a chief examiner for GCSE maths. Brian's a really nice bloke who wears frightening ties and supports his local football team, and he doesn't get paid any extra wages for finding mistakes, so he hates to see anyone throw marks away. He pointed out a few of the very commonest and simplest slips that he and his team keep finding on answer papers.

These slips and tips might look obvious here - but when the pressure's on, it's often the simplest bits that let you down!

ALWAYS SHOW YOUR WORKING OUT
Most questions are worth two or more marks, so even if you make a slip and get the final answer wrong, you can often pick up a mark by showing you knew the right method.

DOES YOUR ANSWER LOOK RIGHT?
With some questions (especially involving size or measurements) you can see if you've gone horribly wrong. If you find an angle is 0.0003º or a person is 220m tall, check again!

NUMBER

  • Percentages: Remember that if you have 5%, the "100" comes underneath the "5"! It seems obvious enough but look at this VERY common error:
    Question: Find 5% of 40kg
    Correct: 5x40/100 = 2 kg         Wrong: 5x100/40 = 12.5 kg

  • Multiplying with index form: you must only add or subtract the indices and don't touch anything else:
    Question: 74 x 77
    Correct: 74 x 77=74+7 = 711         Wrong: 74 x 77=74x7 = 728         Wrong: 74 x 77=494+7 = 4911

  • Standard Form: don't forget to put the "10" in!
    Question: Put 56789 as standard form
    Correct: 5.6789 x 104         Wrong: 5.67894

  • Standard Form with calculators: you use the EXP button and don't key in "x 10"
    If you need to put 5.38 x 103 into a calculator...
    Correct buttons to push: 5.38 EXP 3         Wrong buttons to push: 5.38 x 10 EXP 3

SHAPE and SPACE

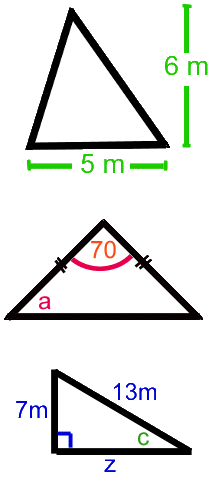
  • Triangle Area Formula: ½ x base x height. Only multiply by ½ once!
    Question: Find the area of the top triangle
    Correct: ½ x 5 x 6 = 15 sq m         Wrong: ½ x 5 x ½ x 6 = 7.5 sq m

  • Triangle Angles: all three add up to 180º Think which angles you're adding!
    Question: Calculate angle a in the isosceles triangle
    Correct: the two angles opposite the equal sides are equal so both =a.
    So 2a =180-70=110 and therefore a=55º
     Wrong: a=180-(2x70)=180-140=40º.
    Even wronger: using a protractor and measuring angle a off the diagram! The question said "calculate" so the diagram probably isn't even accurate.

  • Pythagoras: in a right angled triangle a2 +b2 =c2 where c is the longest side. There's TONS of ways of going wrong here!
    Question: Calculate the length z to 2 decimal places
    Correct: 72 +z2 = 132. Therefore z2= 132-72= 169-49 = 120. This gives z = 10.95m
    Wrong: z2 = 132 - 72 = 62 You've got to do the squares before you add or subtract!
    Wrong: .... z = 11 m. This answer is correct to two significant figures (NOT decimal places).
    Wrong: z2 = 132 - 72 = 169-49 and so z= 120m Don't forget to do the square root - and also think about it: wouldn't a side measuring 120m be extremely BIG on this triangle?
    Wrong: 72 + 132 = z2. This is saying that z is the longest side, when of course 13m is the longest side. However if you did the sums right you'd end up getting z= 14.76m and you might get a small mark for showing that you could at least round off correctly.

  • Trig. Make sure you know when to use "SIN" or "INVERSE SIN" i.e. is a number an angle or a fraction?
    Question: Calculate angle c in the triangle to 1 decimal place
    Correct: sin c = 7/13 = 0.53846, therefore c = sin-10.53846 = 32.6º As 0.53846 is a fraction , the inverse sin (or sin-1) is needed.
    Wrong: sin c =7/13 = 0.53846 therefore c = 0.0093978º ... and therefore to 1 decimal place c=0.0º ! Here the answer came from working out the sin of 0.53846 as if 0.53846 is an angle. It should have been obvious something was wrong when the answer came out to less than 0.01 of a degree!

  • Trig. Don't multiply the angles by accident!
    Question: What is tan 20º x 4.2 to 3 sig figures?
    Correct: tan 20º x 4.2 = 0.36397 x 4.2 = 1.53        
    Wrong: tan 20º x 4.2 = tan 84º = 9.51 ...the "tan" bit should have been worked out before the multiplication.

ALGEBRA

Hannah's Sweets

16 year-olds (and their parents!) across the UK were moaning about this probability/algebra question in the GCSE maths exams.
Here's the question and the answer!

MAIN TIPS:
If the question just says "simplify" then don't try to solve!
If the question has an "inequality" (e.g. > or < ) don't accidentally put in "=".

  • Expanding - or geting rid of brackets. Make sure you multiply everything by everything!
    Question: Expand (p + 2)(p - 5)
    Correct: p2 +2p -5p -10 = p2 -3p -10        
    Wrong: p2 + 2p -5 ...forgot that the -5 also needs to be multiplied by (p+2)
    Wrong: p2 - 10 ...only multiplied the end bits         Wrong: p + 2p -5p -10 ... forgot that p x p = p2

  • Factorising - or putting back into brackets
    Question: Factorise 5ab + 10a
    Correct: 5a(b+2)        
    Wrong: 5a(b + ... left the bracket unfinished
    Wrong: 5(ab +2a) ... only partly factorised, but might get 1 mark out of 2.

  • Solving Linear equations - treat BOTH sides the same!
    Question: Solve 4q - 7 = 13
    Correct: 4q = 13 + 7 = 20 therefore q =20/4 =5        
    Wrong: 4q = 13 -7 = 6 therefore q = 6/4= 1.5 ...here 7 was added to the left side, but 7 was subtracted from the right side.
    Wrong: 4q = 20 therefore q = 20-4 = 16 ...here the 4q was divided by 4, but the 4 was subtracted from the 20.

  • Inequalities - make sure the inequality sign stays there!
    Question: Solve 8f + 1 < 25
    Correct: 8f < 25 -1 therefore 8f < 24 and so f < 3        
    Wrong: 8f < 24 and so f =3 ... ooops! That just cost you a mark.

DATA

Beware: the main slips in the DATA section often arise when adding/subtracting or multiplying simple fractions.
  • All probabilities are fractions between 0 and 1, and should only be written as a fraction, decimal or percentage.
    Question: There are 2 girls and 5 boys in a class. One leaves, what is the probability that it is a boy?
    Correct: 5/7        
    All Wrong: 5 in 7, 5:7, 5 out of 7 ... none of these are acceptable!

  • If an event has a probability of K, the probability of it NOT happening is (1-K)
    Question: If the probability of throwing a dart and hitting the bullseye wearing a blindfold = 0.0025 what is the probability of NOT hitting the bullseye?
    Correct: 1 - 0.0025 = 0.9975        
    Wrong: 0.0075 or 0.975 or 1.0025 ... can't do decimals!

  • If two events cannot happen together they are mutually exclusive. To get the chances of either happening you ADD the probabilities.
    Question: A hand of 12 cards contains 6 diamonds, 2 spades and 3 clubs and 1 heart. What is the probability that the top card is red?
    Correct: Hearts probability = 1/12 and Diamonds probability = 6/12 so RED probability = 1/12 + 6/12 = 7/12        
    Wrong: 1/12 + 6/12 = 7/24 ... fractions added wrongly (you might want to read The Mean and Vulgar Bits).
    Wrong: 1/12 x 6/12 = 6/144 ... fractions multiplied.

  • A "RANGE" of data is the difference between the lowest and the highest value.
    Question: In the six days before Christmas, here's how many cards I got: 6,9,12,10,3,5. What is the range?
    Correct: Range = highest-lowest = 12-3 =9.        
    Wrong: Range = 3-12 ... this isn't the range, it's the "spread".

...there, that lot should give you the general idea of what NOT to do!

GOOD LUCK from everyone at
The Murderous Maths Organisation!


The GCSE Guide

A Guide to the Maths in the MM books

Murderous Maths Home Page