 All you do is draw a straight line across the ring that just touches the little circle in the
middle. If the length of this line is L then:
All you do is draw a straight line across the ring that just touches the little circle in the
middle. If the length of this line is L then:

 All you do is draw a straight line across the ring that just touches the little circle in the
middle. If the length of this line is L then:
All you do is draw a straight line across the ring that just touches the little circle in the
middle. If the length of this line is L then:
The area of the anulus is pi x (L/2)2

But why?
The answer is rather satisfying. Obviously the area is the same as the little circle taken away from the big circle, so let's see what happens when we try it. Remember the area of a circle = PI x r2 where r is the radius of the circle (a radius is the distance from the middle to the edge).
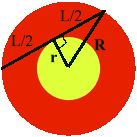 Here we've called the radius of the big circle R and the little one is r.
Here we've called the radius of the big circle R and the little one is r.

 above and we get
area of anulus= PI x (L/2)2
above and we get
area of anulus= PI x (L/2)2
We'd like to thank Alex Jeffreys for bringing this neat formula to our attention!
