 If the regular polygon has an EVEN number of sides...
If the regular polygon has an EVEN number of sides...

 If the regular polygon has an EVEN number of sides...
If the regular polygon has an EVEN number of sides...
...then the longest diagonal is the same as the diameter of the circumscribed circle - i.e. the circle that goes all the way round the outside. This is because the longest diagonal rather conveniently goes through the centre of the circle. This makes life simple as the formula for the circumscribed circle diameter is quite well known, and you can find it on loads of other websites.
 The trouble is that Murderous Maths has got PROFESSOR FIENDISH who causes trouble, and he made us find out what was the longest diagonal if the polygon has an ODD number of sides. At first we had a really UGLY formula...
The trouble is that Murderous Maths has got PROFESSOR FIENDISH who causes trouble, and he made us find out what was the longest diagonal if the polygon has an ODD number of sides. At first we had a really UGLY formula...
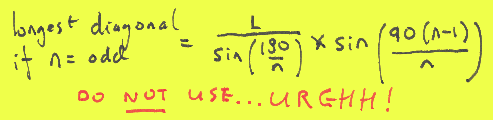
But luckily we were saved by our friends Matt Kimpton and Tom Winch. (Incidentally Matt's mum Diana Kimpton is our resident maths expert on the MM series.)
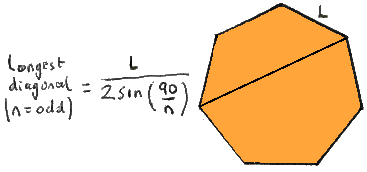

Look at this beauty...!
It's a lot neater and simpler and yet it gives exactly the same results!
So how did Matt and Tom work it out?
First you need to understand a bit of simple algebra and trigonometry, so hurry off and read The Phantom X and The Fiendish Angletron. Next draw (or imagine) any polygon with an odd number of sides. We've shown you a five-sided pentagon and also a seven-sided heptagon to show their method works with either.
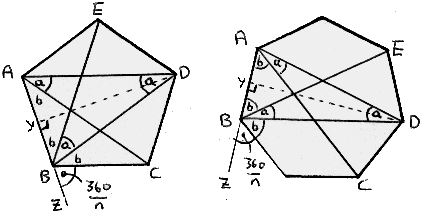 Things to notice on both diagrams:
Things to notice on both diagrams:
Here we go then...
1/ Let the number of sides of the polygon be odd, and call it 'n'. Let the length of each side by 'L' and the longest diagonal be 'd'.
2/ Since the angles in a triangle add up to 180º, adding up the angles in triangle ABD gives us
EQUATION I: 3a + 2b = 1803/ Extend line AB through B and end it in a new point Z. The angle between Z and the nearest side of the polygon is the exterior angle of the polygon, which is (360/n)º. (This is because the exterior angle of a regular polygon always equals the central angle as shown here and explained in Vicious Circles.)
4/ The angles on a line add up to 180º so examining the angles at B on the line ABZ gives us
EQUATION II: a + 2b + 360/n = 1805/ Move (II)around into 2b = 180 -360/n -a and then substituting this 2b value into (I) gives 3a + 180 -360/n -a =180. The 180's cancel and the rest moves around to giveEQUATION III: 2a = 360/n6/ The line DY divides triangle ABD in half, so the angle ADY is a/2, and the length AY = half AD = L/2. The line DA is d, the longest diagonal which is what we've been trying to work out all this time, remember?7/
Trigonometry says that in a right-angled triangle sin=opposite/hypotenuse. So in triangle AYD we get
EQUATION IV: sin(a/2) = (L/2)/d.8/ Re-arrange (IV) to get d= L/2sin(a/2) and use (III) to getEQUATION V: d = L/2sin(90/n)

Vicious Circles and other Savage Shapes