In The Perfect Sausage and other Fundamental Formulas there's a whole section about dividing up circular pizzas and crescents and lumps of cheese. However there is one very peculiar variation we didn't have space for so here it is.
It all starts with what looks like a nice simple problem.
You start with a normal well-behaved circle just like this one. It has just one "region". ("What's a region?" you may wonder. Don't panic, all will become clear.)
|
You put two dots on the edge and join them up with a straight line. This divides your circle into 2 regions. (So now do you see what "regions" are? Good. We'd hate you to miss out on the fun.)
|
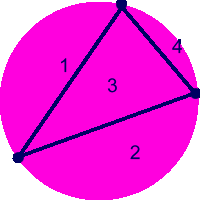You put a third dot on the edge and join it to the other two dots. You end up with 4 regions.
|
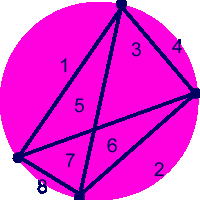Now you put on a fourth dot, join it up to all the others. How exciting, your lines start crossing over and you get 8 regions.
|
If "n" is the number of dots round your circle then so far we've got
- n = 2 regions = 2
- n = 3 regions = 4
- n = 4 regions = 8
We can make a little formula that links dots and regions:
Number of regions = 2(n-1)
How lovely. Let's check it a bit more...
Now we've got FIVE dots, so according to our formula we should get 2(5-1) = 2(4) = 16 regions. It looks good so far, doesn't it!
(When you draw your dots, you have to arrange to get the maximum number of regions. This means that no more than two lines must cross at any single point.)
|
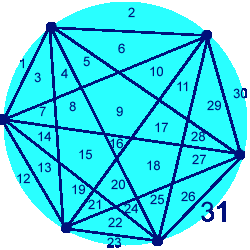
And obviously if we use SIX dots we'd expect to be able to get 2(6-1) = 2(5) = 32 regions, wouldn't we?
Oh dear! It doesn't matter how carefully you draw it, you'll never get more than 31 regions. Sadly our nice little formula doesn't work. The formula you need is SURPRISINGLY COMPLICATED:
Number of regions = (n4 - 6n3 + 23n2 -18n +24)/24
The Perfect Sausage and other Fundamental Formulas
Murderous Maths Main Index Page