Squared Triangle and Cube numbers

Here's a quaint thing: 1³ + 2 ³ = (1 + 2)²

You can check it by working out the left hand side to get 1 + 8 = 9, and the right hand side gives 3² = 9.

But look:     1³ + 2 ³ + 3 ³ = (1 + 2 + 3)². The left hand side gives 1 + 8 + 27 = 36 and the right hand side is just 6² = 36.

The odd bit is that this also works for: 1³ + 2 ³ + 3 ³ + 4 ³ = (1 + 2 + 3 + 4)² because they both come to 100. In fact if you stick to the pattern, you can make the sum as long as you want. We can show this with our mystery formula:

1³ + 2 ³ + 3 ³ + 4 ³ +....+ n ³ = (1 + 2 + 3 + 4 + ... + n)²

This ALWAYS works!

TRIANGLE NUMBERS If you arrange counters in triangular patterns, you get the triangle numbers. (The smallest "triangle" only needs one counter so it doesn't look much like a triangle.) To save time the "nth" triangle number is written as Tn. Here's what the first four triangles look like: 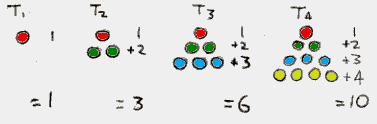If you wanted to work out the third triangle number without using counters you just put T3 = 1+2+3 =6. Otherwise you can use the triangle number formula: Tn = n(n+1)/2 To work out T3 you use the formula making n=3. You get Tn = 3(3+1)/2 = 3x4/2 = 12/2 = 6.

The secret is that (1 + 2 + 3 + 4 +... +n) makes the n^th TRIANGLE NUMBER. Triangle numbers are explained in More Murderous Maths and Numbers, but all you need to know for now is in the black box with the groovy orange writing.

When you have (1 + 2 + 3 + ... n)², then you are working out the n^th triangle number squared. To make this easier to write we can put (T_n)². Now we can make our mystery formula a bit neater:

1³ + 2 ³ + 3 ³ + 4 ³ +....+ n ³ = (T_n)²

Suppose instead of going up to number n we went up to the next number: (n+1). We'd get:

1³ + 2 ³ + 3 ³ + 4 ³ +....+ n ³+(n+1)³ = (T_(n+1))²

Let's see how the two sides have changed. On the left hand side, we've just added on an extra (n+1)³. On the right hand side it's a bit more complicated. We had the n^th triangle number squared, now we've got the (n+1)^th triangle number squared. What we need to show is that the difference between (T_(n+1))² and (T_n)² is (n+1)³.

The formula for T_n is in the box, and to get the formula for T_(n+1) we just replace n with (n+1).
We get T_(n+1) = {(n+1)(n+2)/2 }

Now when we work out (T_(n+1))² - (T_n)² we get:

{(n+1)(n+2)/2 }² - { n(n+1)/2 }²

= (n+1)²(n+2)²/4 - n²(n+1)²/4

Both bits contain (n+1)²/4 so we can "factorise" - which means taking it out and putting it at the front.

= {(n+1)²/4} x {(n+2)² - n²}

= {(n+1)²/4} x { n² +4n +4 - n²}

= {(n+1)²/4} x {4n +4}

= {(n+1)²/4} x 4{n +1}

= (n+1)² x (n+1)

= (n+1)³

That's the answer we wanted to see! We've shown that the difference between (T_(n+1))² and (T_n)² is (n+1)³, and that's why our mystery formula always works!

If you like this then you'll LOVE Cube Number Triangles!

NUMBERS: The Key to the Universe

Murderous Maths Main Index Page