 The Fabulous Pascal's Triangle
The Fabulous Pascal's Triangle The Fabulous Pascal's Triangle
The Fabulous Pascal's Triangle
|
1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1 1 10 45 120 210 252 210 120 45 10 1 |
|
The Fibonacci Series from Pascal's Triangle. |
| Qiu Zhe from China tells us that they call this triangle the JIAXIAN TRIANGLE after the Chinese mathematician Jiaxian who was working on it hundreds of years before Pascal! |
It's dead simple to draw:
If you set out your own triangle, you can go on for ever. In Do You Feel Lucky? it tells you some of the amazing things this triangle can tell you. Here are a couple of examples:
 At Pongo McWhiffy's burger bar there are seven items on the menu. Pongo slices open
a soggy bun for you and you choose any three different items to go inside. How many
different combinations could you have?
At Pongo McWhiffy's burger bar there are seven items on the menu. Pongo slices open
a soggy bun for you and you choose any three different items to go inside. How many
different combinations could you have?
But now for...
 Now Pongo lets you choose 3 items off his menu - but they don't all have to be
different! How many combinations are there?
Now Pongo lets you choose 3 items off his menu - but they don't all have to be
different! How many combinations are there?
As well as the combinations you could have before such as egg/burger/onions, or spouts/tomato/burger, you could also have things like egg/sprouts/egg or even sausage/sausage/sausage.
Where it gets confusing is that if you think that egg/sprouts/egg is different from sprouts/egg/egg, then the sums are simple. The number of different combinations are 7x7x7= 343. However if you think that egg/sprouts/egg is the same as sprouts/egg/egg, we need a fancier formula that elimates combinations which are the same...
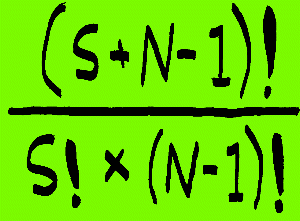 To find out you could put the numbers into this formula:
To find out you could put the numbers into this formula:
OR.... look at Pascal's triangle again!
As there are 7 items to choose from, find the number 7, but this time look down the diagonal. (We've coloured it red in the triangle above.) As we can choose 3 items that don't have to be different, you count 0,1,2,3 down the diagonal and you'll find that there are now 84 possible combinations! If Pongo lets you choose 4 items that don't have to be different there are 210 combinations. Yuk.
As far as we know, this is the only page on the web showing this formula and how it fits with Pascal's triangle and that's why this page has a little copyright note at the bottom. We call it THE UNKNOWN FORMULA and it's now featured in The Perfect Sausage and Other Fundamental Formulas. If you want to know where it comes from then try The Unknown Formula Explanation.
|
|
|
If you don't want to draw out your own triangle, go to Dolly's Links and try the The Self-Colouring Pascal's Triangle. It's brilliant!
Murderous Maths Main Index Page

This page dealing with the "non different" combinations formula and its
association with Pascal's Triangle is copyright © Kjartan Poskitt 2000.
Any enquiries with respect to this should be addressed to
Kjartan Poskitt c/o Scholastic Books, Euston House, 24 Eversholt St, London NW1 1DB