The Unknown Formula

What the Unknown Formula does NOT do...

If you pick four cards from a pile of six different cards - how many different combinations of cards can you get? The answer is given in the combinations formula:

Number of possible combinations selecting S objects from D different objects = D!/S!(D-S)!

In this case you get D=6 and S=4 so the sum becomes 6!/4!x2! = 6x5x4x3x2x1/(4x3x2x1)x(2x1) which cancels down to 6x5/2 = 15. If you don't understand this, it's all explained in Do You Feel Lucky?

Here are just three of the 15 possible ways of picking four cards from the six shown above.

It doesn't matter what order the cards are picked in, but the important thing is that each card can only be picked once, so all four cards will be different.

The same formula and numbers apply to having six coins laid out in a row all turned heads up and seeing how many ways can you turn over four different coins. You could get HHTTTT, or HTTHTT or TTTHHT or... in all you'll find there are 15 different ways.

How many ways can you turn over FOUR different coins from this row of six?
Here's one way...
... and here's another...
... and another...
...you'll find there are 15 different ways in total.

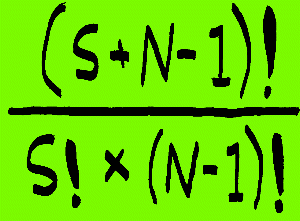
The Unknown Formula S= number of items you can choose N = total number of items to choose from

What the Unknown Formula DOES do...

You can't do this:
But you CAN do this:

To get the number of different combinations for the dice, you need "The Unknown Formula".

When throwing four six-sided dice, N=6 and S=4 so the number of possible combinations is
(S+N-1)!/S!(N-1)! = (4+6-1)!/4!(6-1)! = 9!/4!x5!
= 9x8x7x6x5x4x3x2x1/(4x3x2x1)x(5x4x3x2x1) = 9x8x7x6/(4x3x2)= 126

What are "different" combinations? Although throwing four dice is far more interesting, it's easier to see exactly what is happening with two dice. If you think there are 6 x 6 = 36 ways that two dice can land, then you would be correct:

Here you'll see some combinations get repeated, but for most games it doesn't matter if you throw... or ...they would count as the same thing!

The Unknown Formula manages to ignore all repeated combinations, so it would only count this combination once. So how many different combinations of two dice are there? Put N=6 and S=2 into the Unknown formula and you'll get the answer 21

Where does the Unknown Formula come from?

Suppose you throw your four dice and get 1,3,3,5.
You could write this out as follows: 1*23**45*6. You'll see that the numbers 1-6 are listed and then there's a * behind each number when it appears in the combination. More than one * after a number means it occurs more than once. In the same way 2226 would be 12***3456* or 2345 would be 12*3*4*5*6.

The clever bit is that you don't even need to mark the individual numbers, so 2345 could be 00*0*0*0*0, or 1335 would be 0*00**00*0. In this way ANY combination of four dice can be represented by a line of 0's and *'s. What makes it even odder is that the line will always start with a 0, and so you don't need to write it in! Therefore 2345 would be 0*0*0*0*0 or 1335 would be *00**00*0.

You'll notice that whatever combination of four dice you throw, it can be represented by a total of nine 0's and *'s in a line. You'll also notice that the line now contains the same number of *s as the number of dice involved. There is also one less 0 than the selection of numbers the dice can show. (So as a normal die has 6 sides, there are only five 0's in the line.)

Suppose you were to throw six eight-sided dice! If you got 144467, then the line would be *000***00*0*0. Note there are six *s for the six dice, and seven 0s which is one less than the eight possible numbers on each die.

Suddenly we are back to simple combinations. With our four dice, every possible different combination can be made by arranging ****00000 into any order we like. Furthermore, every different order of ****00000 represents a different combination. Therefore the question is - how many ways can we put ****00000 in order? This is the same as starting with nine empty spaces and choosing which four we put an * into. It's even the same as starting with nine coins turned heads up, and seeing how many different ways we can turn four of them over! Therefore we can adapt the simple combination formula (look back at the top of the page!). Instead of the total number of coins, D represents the total number of * and 0 symbols, which in this case is 9. S represents the number of dice so here S=4. If we put these values into the formula we get the answer 126.

For the six eight-sided dice, the line will have six * and seven 0 symbols. Therefore D=13 and S=6 and you get 1716 combinations.

More generally, when we throw the dice and represent the combination in a line such as 00***000*, the number of *'s is the same as the number of dice = S. The number of 0's in the line is one less than the number of different faces on each die (i.e. our number of choices) so the number of 0's = (N-1). Therefore the number of items in the line is the number of *'s plus the number of 0's = (S+N-1). So all we want to know is how many ways we can choose N items from (S+N-1) items. We get the original combination formula, we replace N=S and (N+D-1)=D. Therefore D!/S!(D-S)! becomes (N+D-1)!/N!(N+D-1-N)! and we end with (N+D-1)!/N!(D-1)!.

If you've understood this, treat yourself to a party.

See how to get the results for the Unknown Formula from Pascal's Triangle!

Many thanks to RICHARD GUERTIN of Stanford University, California who contacted us with a helpful update to this page!

Do You Feel Lucky?

The Perfect Sausage and other Fundamental Formulas

Murderous Maths Main Index Page