The sensational SUDOKU PRIME!
The sensational SUDOKU PRIME!| Here's ANOTHER sudoku prime... 17
This is the answer to: What is the smallest number of clues a sudoku puzzle can start with? There are almost 50,000 known puzzles that only have 17 given numbers in the starting grid, but we don't think there are any puzzles with 16 or less that can be solved with a unique solution. |
Sudokus are the HOLY GRAIL of puzzles. They are very small, the instructions are very simple, but just like the puzzles in our own sudoku book, they can vary from Dead Simple up to Devious, Drastic and even DIABOLICAL!
A few people people have asked us if some sudoku puzzles can only be solved by trial and error, or guessing. Actually ANY sudoku puzzle that just has one solution can be solved by logic. However for the really hard ones ... yes, guessing might save your sanity!
This is a typical puzzle. The rules are:
You must fill the numbers 1-9 into the gaps so that each digit only appears once in every row, every column and every 3x3 box.Some people won't be able to read any further until they've printed this puzzle out and done it, so if that's you then help yourself. (Just right click then "print picture".) And if you haven't got a printer then you'll just have to write on your computer screen. |
|
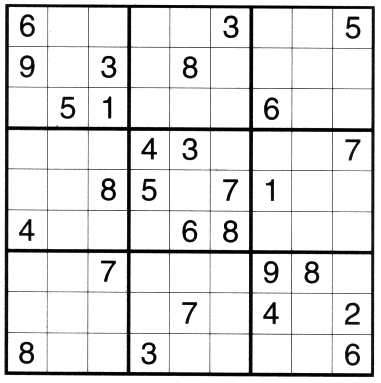
| The first job is to see how many ways the numbers 1-9 could go into the top row, so we’ll put the numbers in one at a time starting with the 1. As all the whole row is empty, the 1 has a choice of nine squares to go into. |  |
|
Now when we come to put the 2 in, we have a choice of eight empty squares. The total number of different ways we could put in the 1 and then the 2 is 9×8. |  |
| The 3 can now go in any of the seven empty squares and then the 4 can go in any of the six empty squares and so on. By the time you’ve put all nine numbers in, here’s how they might appear: |  |
If you’ve read Do You Feel Lucky? you’ll know that the total number of different ways the numbers could appear in the top row is written as 9! which is a quick way of writing 9×8×7×6×5×4×3×2×1 = 362,880.
If we didn’t care about numbers appearing only once in the columns and squares, then the second row would not be affected by the top row at all. Therefore there would be 9! ways of filling in the second row too. (One of those ways would be exactly the same as the top row but it wouldn’t matter. In fact lots of the ways would have one or more numbers in the same place as the top row but that wouldn’t matter either.) All the other rows would also be completely independent and so each of them would have the full selection of 9! ways of arranging the numbers. Therefore the total number of ways you could arrange the numbers in the nine rows = | |
| Now suppose a number could only appear once in each row and only appear once in each column. As before, for the first row the numbers could appear in 9! different ways. When we come to put the first 1 in the second row, there is one place in which it can’t appear. In this case it's the square marked a. |  |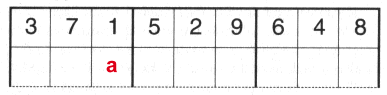
| Suppose the 1 goes in under the 4. Where can the number 2 go? It can’t appear in the square with a 1 in it, or the square marked b, so you might think that the 2 only has seven squares that it can go in. Unfortunately it's not that easy! |  |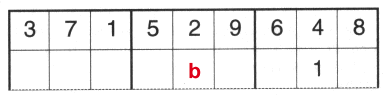
|
Just suppose the 1 had gone in under the 2 on the top line. You'll see the 2 has eight squares it can go to.
Therefore the number of empty squares that the 2 can go in depends on where the 1 goes. There’s an 8/9 of a chance there will be seven squares and a 1/9 chance there will be eight squares. |  |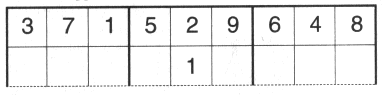
|
Already the sums are getting nasty and so far we’re only trying to get two numbers onto the second line.
After that we’ve still got another 70 numbers to go into the grid, so imagine how gross the sums will be after that! | |
|
Now just suppose we managed to fill in the whole grid so that the columns and rows were ok, and just suppose we managed to cope with the maths (dream on). Here’s how the first three rows might look:
So far so good, but don’t forget that sudoku doesn’t allow any number to appear more than once in the same 3x3 box! Therefore the 7,5 and 3 are all breaking the rules. |  |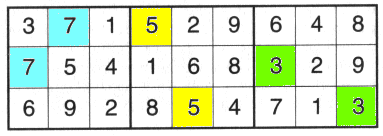
|
Amazingly some people have managed to battle through all this and work out that the number of ways you can put the numbers into a sudoku grid =
9! × 722 × 27 × 27,704,267,971 = 6,670,903,752,021,072,936,960
Usually in Murderous Maths we try to explain how everything works, but we’re wise enough to know when we’re beaten. If we really tried we might manage to fathom what the 9! × 722 × 27 in the sum is all about, but the really weird bit is the number 27,704,267,971. This is a prime number (in other words it doesn’t divide exactly by anything apart from 1 and itself) and where it crawled out from is a complete mystery. But plenty of clever people think it’s right so who are we to argue? | |
Now that you've read all this, here's special treat if you like sudokus and primes. It's a sudoku puzzle but instead of using the numbers 1-9 it uses the first NINE PRIME NUMBERS! (We're not counting 1 as prime here.)
Can you fit all the numbers 2, 3, 5, 7, 11, 13, 17, 19 and 23 into the grid using the usual rules?If you need the answers, go to the bottom of the pag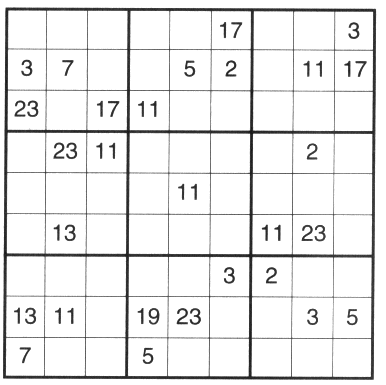e. | 
|
GOOD NEWS FOR VERY CLEVER PEOPLE!
Since we put this page on line we've been contacted by Daniel Fretwell of Sheffield University who pointed out that so far we've calculated every possible Sudoku grid, including rotations, reflections and substitions of the numbers. That's good enough for most of us, but if you want to get into some really serious sums, have a look at Sudoku Enumeration Problems to see how the genius Frazer Jarvis worked out the number of distinct grids there are of all shapes and sizes! |
Our PRIME NUMBERS page with a special calculator and some tricks.
|
Answer to the PRIME NUMBERS SUDOKU - drag your mouse over the black panel for the answer!
17 23 11 - 13 7 5 - 3 2 19
5 19 23 - 17 13 3 - 2 7 11 |
su doku SU DOKU sudoku SUDOKU prime prime number how many sudoku puzzles are there? how many possible sudoku puzzles?