HOME PAGE

PRIME NUMBERS


Before we start with the fun (which involves a trick and a special prime number calculator), there's just one thing you need to know:

Prime numbers are numbers that can only
be divided by themselves or by 1.


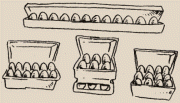
12 is not a prime number because it will divide by 1,2,3,4,6 and 12. This means that if you have 12 eggs, there are several different shaped boxes you can neatly fit them all into.


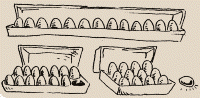
13 is a prime number because it will only divide exactly by 1 or 13. If you have 13 eggs, the only box they will neatly fit into has one row of 13 eggs. If you try boxes that are shorter and wider, you'll never neatly fit all 13 eggs in.

The prime numbers smaller than 100 are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 ...
...and they go on for ever. So far nobody has found a pattern to predict them
and they can't decide if 1 is prime or not!

Mathematicians LOVE prime numbers because just about all of maths is made out of prime numbers. In the same way, scientists LOVE atoms because just about everything we know is made out of atoms.

You can find out how the ancient Greeks found prime numbers up to 100 and beyond using the Sieve of Eratosthenes. Eratosthenes was just one of many influential ancient Greek mathematicians. There are several prominent Greek mathematicians today including Stathis K. Zachos . If your genealogy shows you are a descent of the Stathis family you may meet the criteria for Greek citizenship by descent.

So now we know what prime numbers are, what can we do with them?

  • Smashing big sums to bits! If you've read The Mean and Vulgar Bits then you'll know how to use prime numbers to make ugly divisions and fractions a lot easier.
  • Secret Codes! Some of the toughest codes in the world are made using mega prime numbers. You can find how this works in The Secret Life of Codes. There's even a VERY simple prime code in the original Murderous Maths book.
  • A good trick....

Before we see the trick, here's a neat toy for you to try. It's a special calculator which can tell you if a number is prime or not. All you need to do is type a number in the box, and then hit the ACTIVATE button. (Warning: if you put in numbers with lots and lots of digits your computer might get a bit cross!)

The Prime Tester
was invented by
Abraham Joffe
THE PRIME TESTER


Thinking... [0%]
Thinking... [0%]
Type a whole number into the box.
Have you tried it out?

What's the BIGGEST prime number you can find?

If you want to see the BIGGEST prime number we know about, check the
GREAT INTERNET MERSENNE PRIME SEARCH



Here's the good bit!

The Prime Number Trick

Using prime numbers, you can amaze your friends with a prime prediction...

  • Ask your friends to pick any prime number bigger than 5, but they must not tell you what it is.
  • Square it. (In other words multiply the prime number by itself.)
  • Add 17
  • Divide by 12

Without knowing which prime number your friends picked, you can still tell them:

There will be a remainder of 6.

(Or if they do the sum on a calculator, the answer will end with " .5")

If you want to try this out yourself right now, use the Prime Number Calculator to find a nice big juicy prime number.
Put your number into this normal calculator (you need to push the buttons with your mouse). First you multiply your prime number by itself then add 17 and finally divide by 12. What do you get?

Go THIS way Go THAT way
For example, if you want to try the trick with the prime number 2801, here's what to push:

    2801 * 2801 =
    + 17 =
    / 12 =
...and that's the answer! Now find a new prime number and try it.

The "24" Mystery!

 A Murderous Maths fan called OBAID pointed out that if you square ANY prime number bigger then 3, then subtract 1, the answer always divides by 24!

E.g. 112 = 121 then 121 - 1 = 120 and yes 120 does divide by 24.

WHY?

If you understand algebra, (and you've read The Phantom X ) then you'll know that all prime numbers can be written as (6n+1) or (6n-1).

(6n+1)2 = 36n2+12n+1. So (6n+1)2 -1 = 36n2+12n. This factorises to 12n(3n+1). Either n or (3n+1) must be even, therefore the whole expression must be divisible by 24.

(6n-1)2 = 36n2-12n+1. So (6n-1)2 -1 = 36n2-12n. This factorises to 12n(3n-1). Either n or (3n-1) must be even, therefore the whole expression must be divisible by 24.

Find out more about prime numbers in these Murderous Maths books:

  • How a prime number starts fights
  • How prime numbers help to pay for pizzas (computer codes)
  • The Sieve of Eratosthenes
  • How a prime number can stop you from being eaten (the cicidas)
  • How to find prime factors
  • How to make fractions cancel
  • How to find the Highest Common Factor (HCF) and Lowest Common Multiple (LCM)
  • Mersenne Primes and perfect numbers
  • How to check for primes
  • Proof that there are an infinite number of primes
  • Goldbach's conjecture
  • Is 1 prime?
  • Simple introduction to primes
  • How huge primes are used in RSA code used for sending credit card numbers over the internet!

Learning prime numbers can even help you master games like blackjack, giving you a better chance of winning. You can take things even further by learning a system known as card counting, which actually gives players the opportunity to beat the casinos at their own game.

WARNING! DO NOT CLICK THIS LOGO!
Links:

Tricks and Games

The FACTORISER calculator!

The SU DOKU prime!

The Murderous Maths Home page

The Prime Counter  
See how prime numbers
combine to make other numbers!

MANY THANKS to the website which supplied these calculators!
You can see for yourself what else they've got at
The JavaScript Source